
CS231n Lecture3 유튜브 강의 링크
CS231n Lecture3 pdf 자료
🚀 개요
Loss Fuction을 통한 w(가중치) 최적화
-
SVM Loss
-
Softmax
-
Optimization
Multi class SVM Loss

w(가중치)가 좋은지 나쁜지 평가하기 위한 방법이 필요하다. score를 통해 w를 정량화하는 방법이 Loss Function를 통한 최적화이다.
- Loss Fuction (손실함수)
예측값과 실제값의 차이인 loss를 도출하는 함수다. loss fuction을 통해 w(가중치)가 얼마나 나쁜지 정량적으로 판단할 수 있다. loss가 낮을 수록 그 classifier의 성능이 좋다고 판단할 수 있다.
- Optimization (최적화)
loss fuction를 최소화할 수 있는 parameter를 찾는 방법을 의미한다. 어떤 w의 loss가 가장 적은지 판단하여 실제값과 loss의 차이를 줄일 수 있다.
Loss Fuction의 계산 과정은 다음과 같다.

-
Sj = 오답 클래스의 예측 점수
-
Syi = 실제 정답 클래스의 예측 점수
SVM Loss는 스코어간의 차이에 주목한다. 뒤에 따라오는 1 값은 Safty margin으로, 정답 클래스의 예측 점수가 오답 클래스의 예측 점수보다 최소한 얼마나 커야하는지 말해준다.
SVM Loss 그래프는 경첩과 비슷하게 생겨서 Hinge loss 라고도 부른다. 어떤 카테고리에 대하여 Syi의 값이 (Sj + 1)의 값보다 크면 loss는 0이며, 이미지를 잘 분류한다고 할 수 있다. 그러나 그게 아닐 경우 Syi의 값이 작아질 수록 loss 값이 커지는 모습을 확인할 수 있다.
SVM Loss를 직접 계산해 본 결과는 다음과 같다.

loss가 0에 가까울 수록 classifier의 성능이 좋다고 할 수 있다. 그러나 고양이, 차, 개구리를 분류하는 과정에서 loss의 평균값은 5.27이기 때문에 별로 좋은 score가 아니다.

loss의 값이 0이 되도록 하는 w는 유일하지 않다. w가 2w, 3w, 4w가 되어도 loss의 값은 변함이 없다.

고양이, 차, 개구리를 분류하는 과정에서 2w가 되어도 loss의 값은 0이 된다.
이렇게 단순하게 loss의 값이 0이 되는 w를 찾는 것은 training data에만 맞는 loss fuction을 구하는 것과 같다. training set의 loss가 줄어들더라도 우리가 실제로 넣고자 하는 test set에서도 loss가 줄어들지는 알 수 없기 때문에 overfitting 문제가 발생할 수 있다.

-
파란 점 : training data
-
초록 점 : test data
training set의 loss 값을 0으로 만든 분류기는 파란색 선과 같다. 저 파란색 선은 test data가 들어왔을 때 overfitting 문제가 나타난다. 그래서 우리는 training data에도 잘 들어맞고, test data에도 잘 들어맞는 초록색 선과 같은 classifier를 지향해야한다.
Overfitting (과적합)
너무 과도하게 데이터에 대해 모델을 learning한 경우를 의미한다. 우리가 사실 원하는 정보는 기존에 알고 있는 데이터에 대한 것들이 아니라 새롭게 우리가 알게되는 데이터에 대한 것들을 알고 싶은 것인데, 정작 새로운 데이터에 대해서는 하나도 못맞추고, 즉 제대로 설명할 수 없는 경우라면 그 시스템은 그야말로 무용지물이라고 할 수 있을 것이다.
우리는 단순하고 최대한 간결한 classifier를 통해 training set을 넣었을 때만큼 test set을 넣었을 때도 잘 동작할 수 있도록 결과를 도출해야 한다. 여기서 Regularization을 사용하여 loss function에 넣어준다.

regularization은 예측모델(W)이 복잡한 고차 다항식을 선택할 때 페널티를 주어서, 단순한 저차 다항식을 선택하도록 만든다. 즉 training data에 완전히 fit하는 overfitting 문제가 나타나지 못하도록 페널티를 주는 것이다.
- λ : R(W)의 값을 맞춰주기 위한 hyperparameter이다. 너무 큰 값이면 지나치게 간결해져서 loss 값을 구하는 의미가 없어지고, 너무 작은 값이면 Regularization 의미가 없어지기 때문에 잘 설정해야한다.
Regularization에는 L2 regularization, L1 regularization, Dropout 등등이 있지만, 일반적으로 많이 사용되는 L2에 대해서 알아볼 예정이다.

L2는 가중치 값이 비교적 균일하게 분포되어 있을 때 덜 복잡한 것으로 간주한다. 가중치 조합 w1 = [0, 0, 0, 1] 과 w2 = [0.25, 0.25, 0.25, 0.25]가 있다고 할 때, 균일하게 분포되어 있는 w2 값을 선택한다. x의 모든 원소가 골고루 영향을 미치는 것을 선호하는 것이다.
또다른 classifier인 Softmax Classifier은 SVM과는 다른 방법으로 loss를 계산한다.

SVM Loss에서는 score 자체의 의미를 파악하기 보다는 단순하게 정답 클래스의 예측 점수가 오답 클래스의 예측 점수보다 높기를 기대했다. 그러나 softmax classifier는 클래스 별로 확률 분포를 얻어 예측 점수 자체에 의미를 부여한다.
loss 연산 과정은 다음과 같다.

주어진 score에 대해 exp 연산을 거쳐서 점수를 반환한다. 산출된 값을 -log 연산을 취해 최종 확률 분포를 계산한다. 이때 exp연산을 거치는 계산이 softmax 연산 (multinomial logistic regression)에 해당한다.
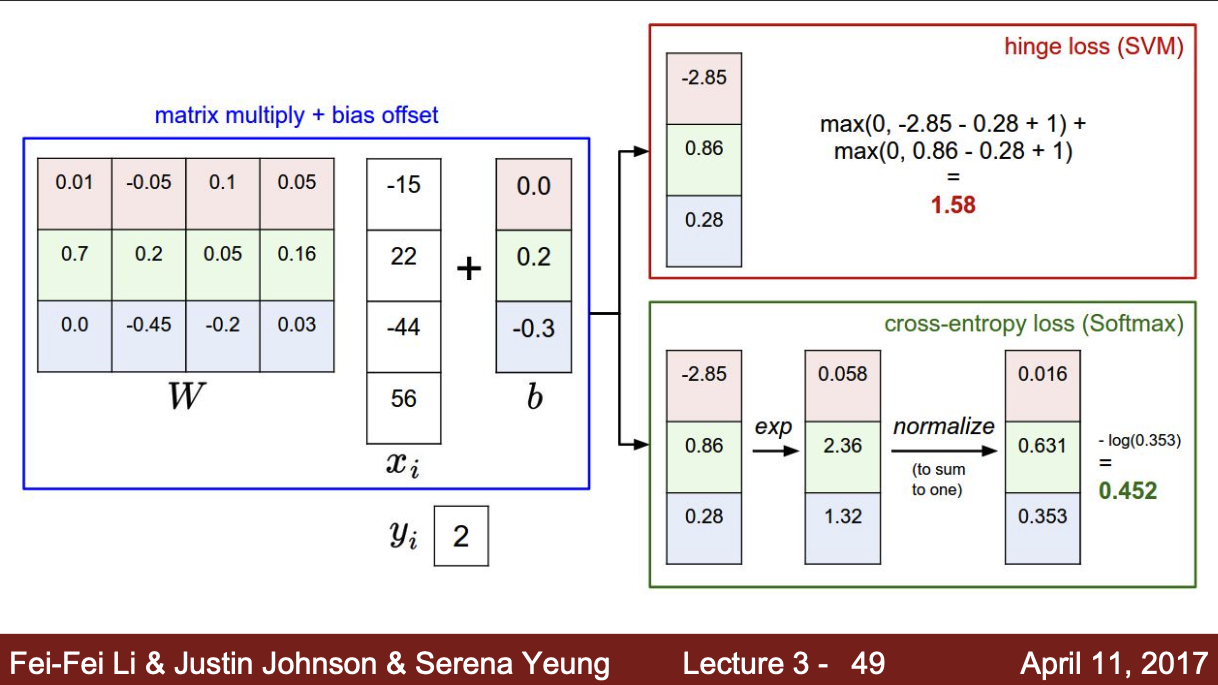
SVM과 softmax를 비교한 그림이다. SVM은 loss의 값이 0이 되는 순간, 더 이상 성능 개선이 이루어지지 않는다. 정답 클래스의 예측 점수가 오답 클래스의 예측 점수보다 높으면 자기 할 일이 끝난 것이다. 그러나 softmax의 경우 최대한 확률을 높이기 위해 연산이 반복되며 성능이 향상된다. 따라서 웬만해서는 loss의 값이 0이 아니라 0에 근접한 값으로 나타난다.
Optimization은 loss의 값을 최소화하는 최종 w를 찾아내기 위한 과정이다.

고지가 높은 산에서 내려갈 때 우리는 반복적인 행동을 통하여 산을 내려간다. 산의 높이를 loss, 우리의 위치를 w라고 할 때 우리의 목표는 loss가 0인 산의 밑바닥에 도착하는 것이다. 우리는 loss가 적은 방향으로 w의 값을 변화시키면서 산을 내려가는데 Optimization을 통해 효율적으로 산을 내려가고자 할 것이다.

Optimization의 가장 단순한 방법은 Random search로, 임의의 w를 계산하여 모든 loss를 비교하는 방식이다. CIFAR-10에서 test set을 넣어본 결과 15.5%의 처참한 정확도가 나온다. 참고로 2017년 당시 현대 최신 기술로는 95%의 정확도가 나온다고 한다.

두 번째 방법은 Follow the slope 방법이다. 우리가 서있는 땅의 기울기를 구하여 어느 방향으로 갈 지를 결정하는 것을 말한다. 여기서 기울기는 어떤 함수에 대한 미분값을 의미한다. 단순해서 잘 동작하며 NN, Linear Classifier 학습에 많이 사용된다.

다음은 Numerical gradient를 이용하여 기울기를 구하는 방법이다. w에 작은 값의 h를 더해 loss를 계산한다.

그러나 이렇게 일일히 함수를 계산하는 것은 매우 비효율적이기 때문에, 우리는 Analytic gradient를 통해 식 하나로 기울기를 계산한다.
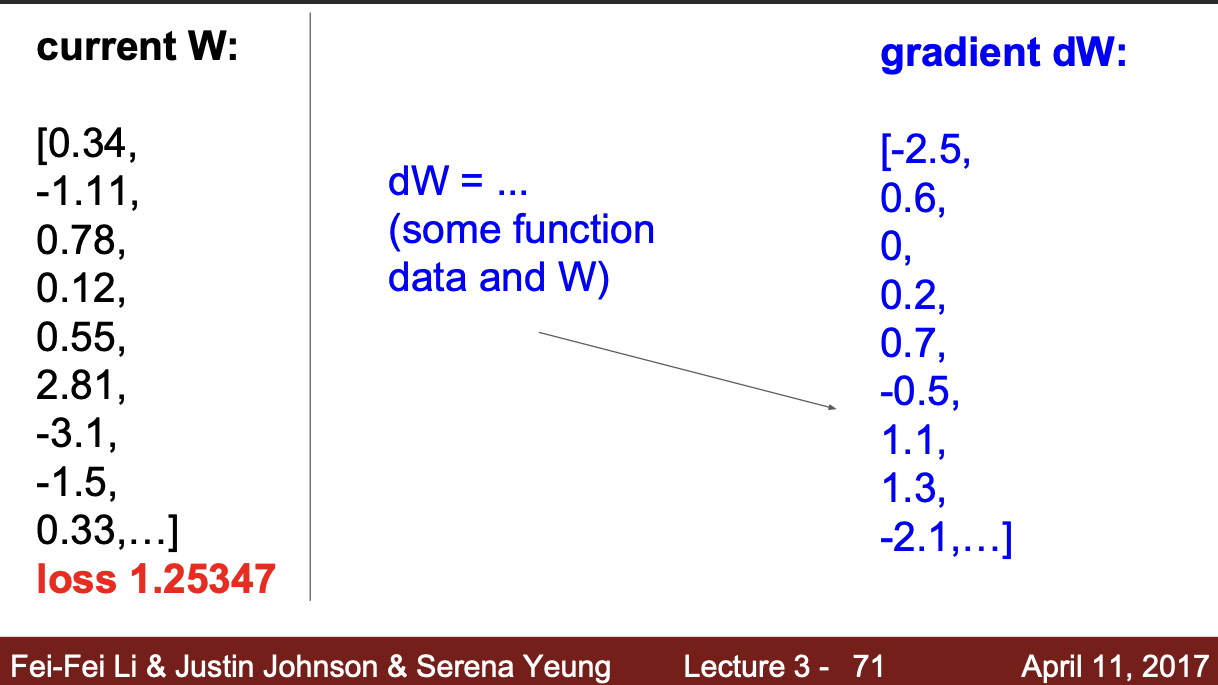
Analytic gradient에서는 함수와 가중치 w만 있으면 기울기를 바로 구할 수 있다.

즉, Numerical gradient는 느리고 정확한 값은 아니지만, 계산이 쉽다. 그러나 Analytic gradient는 빠르고 정확한 값을 얻을 수 있지만, 코드 작성이 복잡해서 에러가 발생하기 쉽다.
정리하자면 우리는 기울기를 구하고, loss의 최소값을 구해야하기 때문에 기울기가 증가하는 반대 방향으로 움직이면서 loss의 최소값을 찾는다.

Gradient Descent를 통해 가장 적절한 가중치를 찾아낼 수 있다.
evaluate_gradient을 통해 미분값을 계산하고 weights에서 (step_size * 기울기) 만큼 빼준다. 뺄셈을 하는 이유는 기울기가 증가하기 때문에 반대로 감소하도록 해서 조금씩 이동하여 최종 loss의 값을 얻고자 함이다. Step_size는 어느 정도의 크기로 이동할 것인지 보여주기 때문에 학습 속도에 큰 영향을 미치는 중요한 hyperparameter이다.
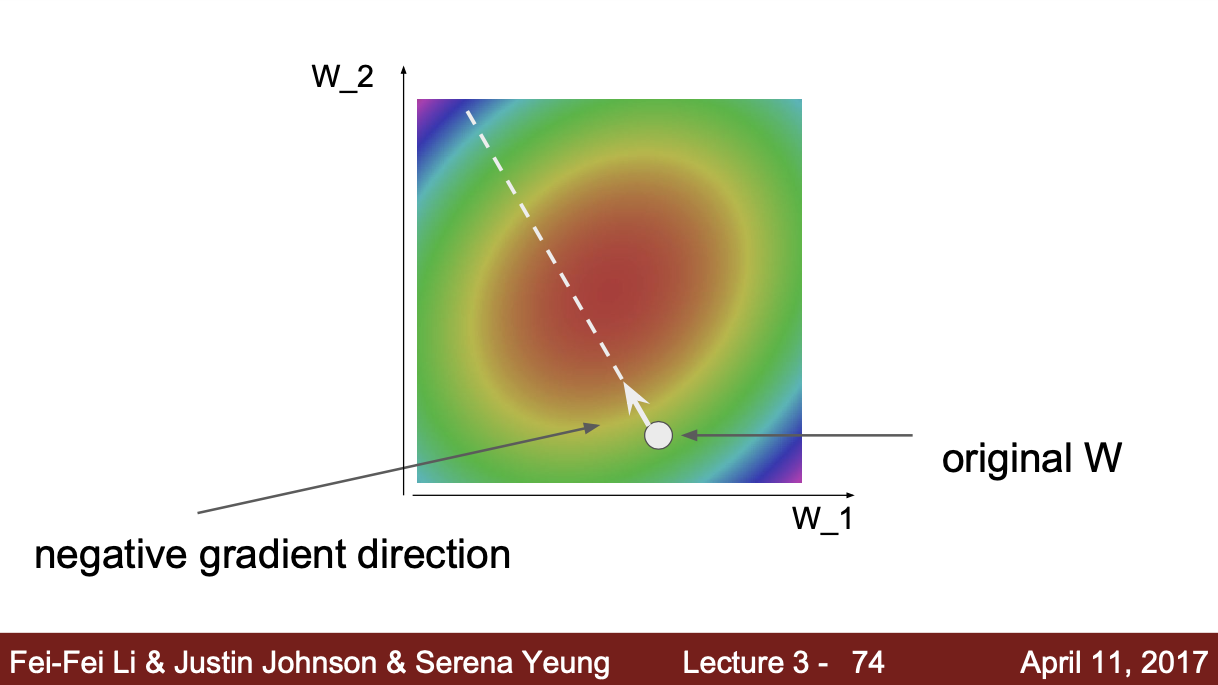
다음 그림은 2차원 공간에서 loss function이 그릇 모양이라고 가정을 할 때다. 빨간색 영역은 loss의 값이 낮은 부분, 파란색 영역으로 갈 수록 loss의 값이 커진다. w의 위치가 초록색 영역에 있다면 w는 빨간색 영역으로 가기 위해 gradient를 반복하여 계산한다. 따라서 매 step 마다 w는 조금씩 -gradient 방향으로 이동하여 w의 위치를 업데이트한다. 이 과정을 update rule이라고 한다.

Gradient Descent를 계산할 때 데이터의 수가 클수록 시간이 오래 걸린다. Minibatch(데이터의 일부분)에 대한 기울기를 통해 실제 loss 값과 gradient를 추정하여 w를 업데이트하는 방식이다.

x, y, Softmax/SVM, Regularization 등의 값을 조절할 수 있는 실습 사이트이다.
이미지를 분류하기 위해서는 이미지의 Feature(특징)을 추출해야 한다.
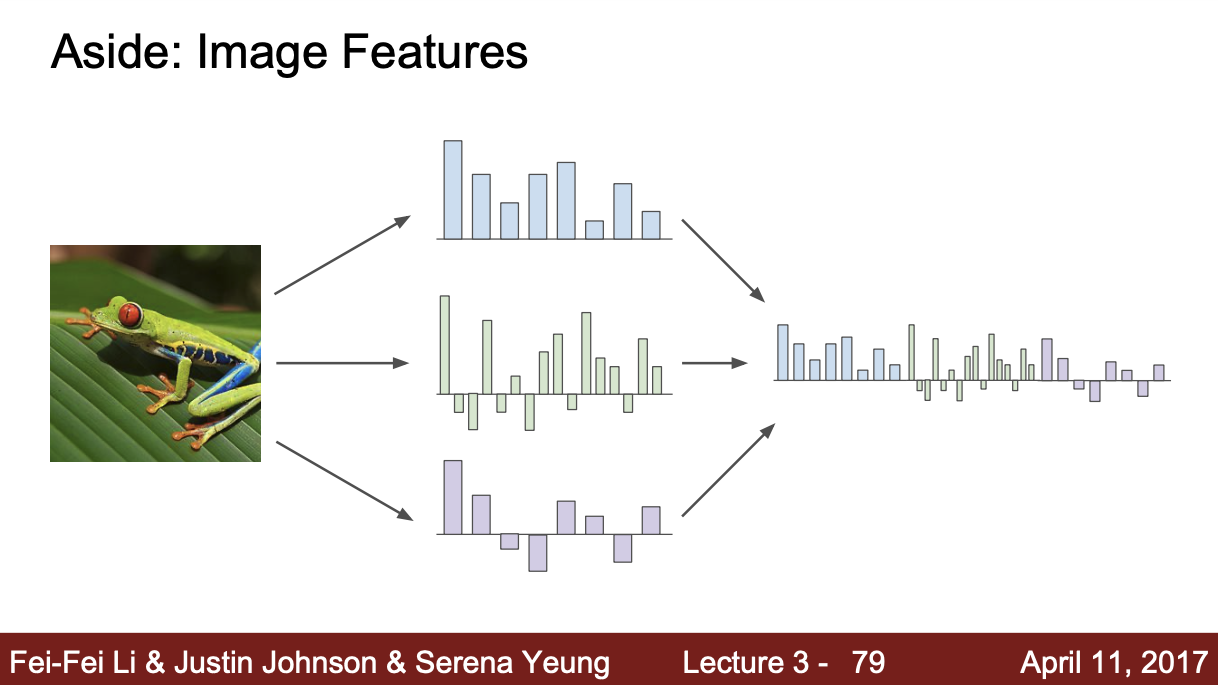
이미지의 특징을 특징 벡터로 변환한다.

왼쪽 그림에서 linear classifier로 결정계를 구분할 수 없기 때문에 Feature Transform(특징변환)을 하여 점들을 오른쪽 그림과 같이 선형 벡터로 변환한다. 오른쪽 그림에서 이제 선형함수로 분리할 수 있게 되었다.
그렇다면 어떤 방식으로 이미지를 feature transform 할 수 있을까?
-
Color Histogram : 특정 색에 해당하는 픽셀의 수를 계산하여 히스토그램으로 표현
-
HIstogram of Oriented Gradients (Hog) : 이미지를 8x8 픽셀로 나누어 가장 지배적인 edge를 찾는다. Edge를 양자화시켜 edge orientation 히스토그램으로 표현한다.
-
Bag of Words : 이미지를 작게 잘라 시각 단어로 표현한 후,K-means 알고리즘으로 1천개의 중심점을 갖도록 학습을 한다. 이미지의 시각 단어의 발생 빈도를 인코딩하여 이미지의 특징을 추출한다.
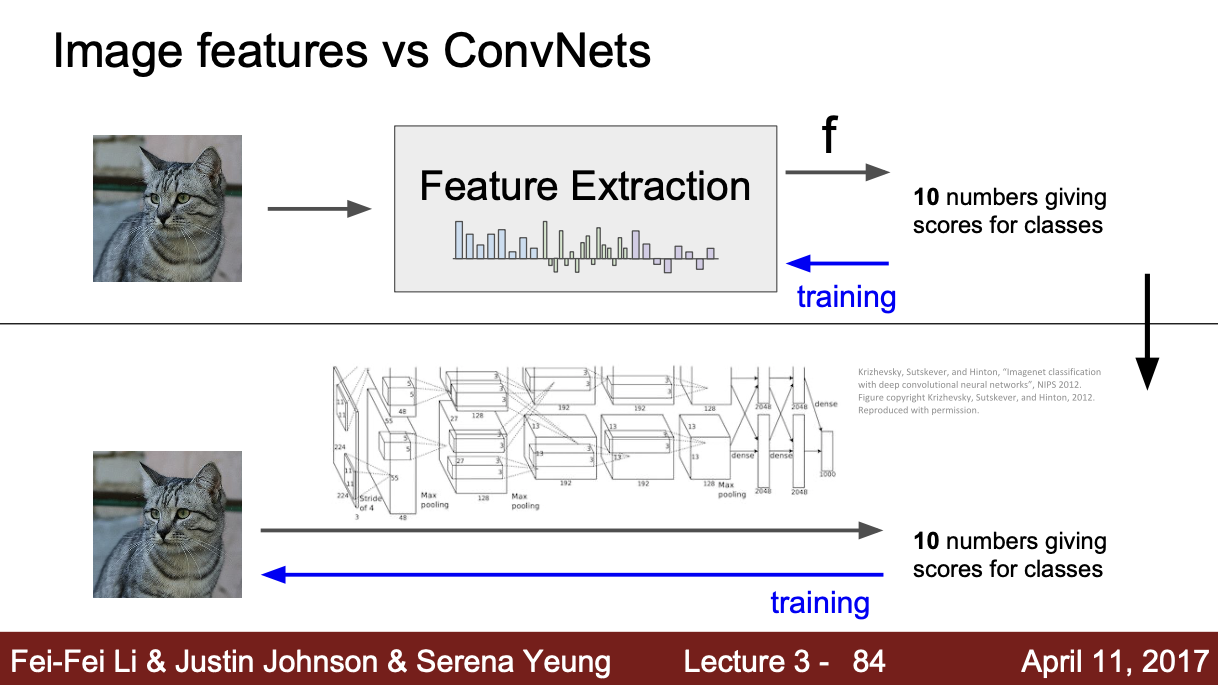
2012년까지는 Image feature을 추출하는 것이 중요했지만, AlexNet이 나온 뒤로는 layer을 쌓으면서 데이터로부터 특징을 직접 추출하여 학습하는 방식을 사용한다. Linear classifier, 가중치를 한 번에 학습하기 때문에 CNN의 구조를 잘 짜는 것이 더욱 중요해졌다.
참고
*[CS231n] Lecture 3 - Loss Suctions and Optimization*
*[풀잎스쿨] CS231n 3강(1) Loss Functions*
*[풀잎스쿨] CS231n 3강 (2) Optimization & Image Features*
*[CS231n] 3. Loss Functions and Optimization*
누구나 이해할 수 있는 딥러닝 - cs231n 3강(Loss Functions and Optimization)